Bismillah...
Sahabat baiq, kembali saya akan berbagi rangkuman materi matematika kelas VIII (delapan) Kurikulum 2013 yaitu tentang Lingkaran. Selamat Belajar!
Lingkaran adalah himpunan titik-titik yang berjarak sama terhadap satu titik tetap yang dinamakan titik pusat lingkaran.
Baca Juga:
A. Unsur-unsur Lingkaran
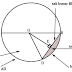
Keterangan:
1. Titik O = pusat lingkaran
2. Garis OA =OB = OD = jari-jari lingkaran
3. AB = diameter lingkaran
4. Garis lurus BD = tali busur
5. Garis lengkung AD dab BD = busur
6. Garis OE = apotema
7. Daerah yang dibatasi oleh dua jari-jari dan satu busur = juring ⇨ misal AOD
6. Daerah yang dibatasi oleh sebuah tali busur dan dua jari-jari = tembereng (yang diarsir)
B. Keliling dan Luas lingkaran
r = jari-jari lingkaran
d = diameter lingkaran
π = 22/7 atau 3,14
C. Panjang Busur dan Luas Juring
Luas tembereng = luas juring AOD – luas segitiga AOD
D. Sudut Pusat dan Sudut Keliling
Perhatikan gambar di atas
∠AOB = sudut pusat
∠ACB = sudut keliling
Sudut pusat dan sudut keliling saling berhubungan jika sama-sama menghadap busur yang sama.
Terlihat bahwa ∠AOB menghadap busur AB, ∠ACB juga menghadap busur AB,
sehingga : ∠AOB = 2 x ∠ACB
E. Segiempat Tali Busur
Segiempat Tali Busur adalah segiempat yang dibatasi oleh empat tali busur dimana keempat titik sudutnya menyinggung sisi lingkaran. Jumlah dua sudut yang berhadapan adalah 180o.
∠A + ∠C = 180o
∠B + ∠D = 180o
F. Sudut Antara Dua Tali Busur
∠ AEC = 1/2 ( ∠ BOD + ∠ AOC )
Pada gambar di atas: BC dan AD diperpanjang sehingga berpotongan di P, maka:
∠ APC = ∠ BPD = 1/2 ( ∠ BOD - ∠ AOC )
G. Garis Singgung Lingkaran
Garis singgung lingkaran adalah garis yang memotong lingkaran di satu titik dan tegak lurus dengan jari-jari yang melalui titik singgungnya. Garis a adalah garis singgung lingkaran yang menyinggung lingkaran di titik A. Garis a tegak lurus OA.
Maka panjang AB = √ OB2 - OA2
1. Garis singgung persekutuan dalam dua lingkaran
R = jari-jari lingkaran; P dan r = jari-jari lingkaran Q; Panjang AB = CQ.
Panjang garis singgung persekutuan dalam AB adalah: AB = √PQ2 − (R + r)2
2. Garis singgung persekutuan luar dua lingkaran
AB disebut garis singgung persekutuan luar dua lingkaran P dan Q.
R = jari-jari lingkaran; P dan r = jari-jari lingkaran Q; Panjang AB = CQ.
Panjang garis singgung persekutuan luar AB adalah: AB = √PQ2 − (R - r)2
H. Lingkaran Dalam dan Lingkaran Luar Segitiga
1. Lingkaran Dalam Segitiga
2. Lingkaran Luar Segitiga
Baca juga:
Sahabat baiq, kembali saya akan berbagi rangkuman materi matematika kelas VIII (delapan) Kurikulum 2013 yaitu tentang Lingkaran. Selamat Belajar!
Lingkaran adalah himpunan titik-titik yang berjarak sama terhadap satu titik tetap yang dinamakan titik pusat lingkaran.
Baca Juga:
A. Unsur-unsur Lingkaran
Keterangan:
1. Titik O = pusat lingkaran
2. Garis OA =OB = OD = jari-jari lingkaran
3. AB = diameter lingkaran
4. Garis lurus BD = tali busur
5. Garis lengkung AD dab BD = busur
6. Garis OE = apotema
7. Daerah yang dibatasi oleh dua jari-jari dan satu busur = juring ⇨ misal AOD
6. Daerah yang dibatasi oleh sebuah tali busur dan dua jari-jari = tembereng (yang diarsir)
B. Keliling dan Luas lingkaran
- Keliling lingkaran = 2πr = πd
- Luas lingkaran = πr2 = π ( 1/2 d )2 = 1/4 π d2
r = jari-jari lingkaran
d = diameter lingkaran
π = 22/7 atau 3,14
C. Panjang Busur dan Luas Juring
Luas tembereng = luas juring AOD – luas segitiga AOD
D. Sudut Pusat dan Sudut Keliling
Perhatikan gambar di atas
∠AOB = sudut pusat
∠ACB = sudut keliling
Sudut pusat dan sudut keliling saling berhubungan jika sama-sama menghadap busur yang sama.
Terlihat bahwa ∠AOB menghadap busur AB, ∠ACB juga menghadap busur AB,
sehingga : ∠AOB = 2 x ∠ACB
E. Segiempat Tali Busur
Segiempat Tali Busur adalah segiempat yang dibatasi oleh empat tali busur dimana keempat titik sudutnya menyinggung sisi lingkaran. Jumlah dua sudut yang berhadapan adalah 180o.
∠A + ∠C = 180o
∠B + ∠D = 180o
F. Sudut Antara Dua Tali Busur
∠ AEC = 1/2 ( ∠ BOD + ∠ AOC )
Pada gambar di atas: BC dan AD diperpanjang sehingga berpotongan di P, maka:
∠ APC = ∠ BPD = 1/2 ( ∠ BOD - ∠ AOC )
G. Garis Singgung Lingkaran
Garis singgung lingkaran adalah garis yang memotong lingkaran di satu titik dan tegak lurus dengan jari-jari yang melalui titik singgungnya. Garis a adalah garis singgung lingkaran yang menyinggung lingkaran di titik A. Garis a tegak lurus OA.
Maka panjang AB = √ OB2 - OA2
1. Garis singgung persekutuan dalam dua lingkaran
R = jari-jari lingkaran; P dan r = jari-jari lingkaran Q; Panjang AB = CQ.
Panjang garis singgung persekutuan dalam AB adalah: AB = √PQ2 − (R + r)2
2. Garis singgung persekutuan luar dua lingkaran
AB disebut garis singgung persekutuan luar dua lingkaran P dan Q.
R = jari-jari lingkaran; P dan r = jari-jari lingkaran Q; Panjang AB = CQ.
Panjang garis singgung persekutuan luar AB adalah: AB = √PQ2 − (R - r)2
H. Lingkaran Dalam dan Lingkaran Luar Segitiga
1. Lingkaran Dalam Segitiga
2. Lingkaran Luar Segitiga
Demikian ulasan tenteng rangkuman materi Lingkaran Matematika SMP/MTs Kelas VIII Semester 2 Kurikulum 2013. Terimakasih sudah berkunjung dan semoga bermanfaat.
- Rangkuman Materi Matematika SMP/MTs Kelas VII K13
- Rangkuman Materi Matematika SMP/MTs Kelas VIII K13
- Rangkuman Materi Sistem Koordinat Cartesius SMP/MTs
Materi Lingkaran SMP/MTs Kelas 8 Kurikulum 2013
 Reviewed by My Profile
on
6:36 AM
Rating:
Reviewed by My Profile
on
6:36 AM
Rating:
 Reviewed by My Profile
on
6:36 AM
Rating:
Reviewed by My Profile
on
6:36 AM
Rating:












No comments:
Note: Only a member of this blog may post a comment.