Persamaan Linear Satu Variabel dan Pertidaksamaan Linear Satu Variabel (Part 3)

Bismillah....

Postingan kali ini adalah lanjutan dari materi Persamaan Linear Satu Variabel (PLSV) dan Pertidaksamaan Linear Satu Variabel (PtLSV) yang sudah di posting sebelumnya. Bagi adik-adik yang belum mempelajari dan mengunduh materi sebelumnya silahkan masuk ke Persamaan Linear Satu Variabel (Part 1) yang membahas tentang kalimat tertutup dan kalimat terbuka dalam Matematika. Selain Itu juga bisa masuk ke Persamaan Linear Satu Variabel (Part 2) yang membahas tentang Persamaan Linear Satu Variabel (PLSV) dan penyelesaiannya. Dan pada postingan kali ini kita akan membahas tentang materi Pertidaksamaan Linear Satu Variabel (PtLSV) dan penyelesaiannya. 

Baiklah silahkan dibaca dan dipahami materinya dibawah ini.

C. Pertidaksamaan Linear dengan Satu Variabel (PtLSV)

1) Pengertian Ketidaksamaan

Hubungan antara bilangan yang menggunakan lambang >, <,  ≤, dan ≥. 

     Contohnya adalah :  3 < 6 atau 4 > 1

     

2)  Pengertian Pertidaksamaan Linear dengan Satu Variabel (peubah)
Perhatikan kalimat-kalimat matematika berikut :

     a. 2x < - 5         b. 2y ≥ y – 5

Kalimat-kalimat terbuka di atas menggunakan tanda penghubung < (kurang dari) dan ≥ (lebih dari sama dengan). Kalimat seperti ini disebut dengan pertidaksamaan. Masing-masing pertidaksamaan diatas hanya memiliki satu variabel (peubah) yaitu x dan y, maka pertidaksamaan ini disebut dengan pertidaksamaan dengan satu variabel. Setiap variabel pada pertidaksamaan di atas berpangkat 1 (dalam aljabar, pangkat satu tidak dituliskan) sehingga pertidaksamaan di atas dinamakan dengan pertidaksamaan linear.

3) Penyelesaian Pertidaksamaan dengan Mencari terlebih dahulu Persamaannya

Contoh:

Tentukan penyelesaian dari pertidaksamaan 2y – 5 < 3

Penyelesaian:

Penyelesaian dari 2y – 5 < 3 jika y variabel/peubah pada bilangan cacah dapat ditentukan sebagai berikut:

2y – 5 < 3

⇔ 2y – 5 + 5 < 3 + 5 (ruas kiri dan kanan ditambah bilangan 5)

⇔ 2y < 8                         (hasil penjumlahan dengan bilangan 5)

⇔ 1/2 x 2y < 1/2 x 8 (ruas kiri dan kanan dikali bilangan 1/2 )

⇨ y < 4                         (hasil perkalian dengan bilangan 2)

Jadi himpunan penyelesaiannya adalah {0, 1, 2, 3)

4) Penyelesaian Pertidaksamaan dengan aturan Memperoleh Pertidaksamaan yang Ekuivalen

• Tanda pertidaksamaan tidak berubah jika kedua ruas ditambah, dikurang, dikalikan atau dibagi dengan bilangan yang sama

          Contoh:

           x – 8 < 12

          ⇔ x – 8 + 8 < 12 + 8 (kedua ruas di tambah bilangan 8)

          ⇔ x < 20                         (hasil penjumlahan dengan bilangan 8)

          Perhatikan tanda pertidaksamaan kurang dari (<) tidak berubah. 

• Tanda pertidaksamaan berbalik/berubah jika kedua ruas dikali atau dibagi dengan bilangan negatif yang sama

          Contoh:

          - 1/3  y + 8 < 6

          ⇔ - 1/3  y + 8 – 8 < 6 – 8 (kedua ruas ditambah dengan bilangan 8)

          ⇔ - 1/3  y < -2                 (hasil penjumlahan dengan bilangan 8)

          ⇔ - 1/3  y  x (-3) < -2 x (-3) (kedua ruas dikali dengan bilangan -3)

          ⇔ y > 6                                 (hasil kali dengan bilangan -3)

Perhatikan tanda pertidaksamaan, karena kedua ruas dikali dengan bilangan negatif yang sama yaitu (-3), maka tanda pertidaksamaan yang tadinya kurang dari (<) berubah menjadi lebih dari (>).

5)  Menggambar Grafik Himpunan Pertidaksamaan pada Garis Bilangan

     Contoh:

     Gambarlah grafik dari himpunan penyelesaian pertidaksamaan 4y + 8 ≤ y + 17, 

     dan y ε bilangan cacah.

     Penyelesaian:

     4y + 8 ≤ y + 17

     ⇔ 4y + 8 – 8 ≤ y + 17 – 8

     ⇔ 4y ≤ y + 9

     ⇔ 4y – y ≤ y + 9 – y 

     ⇔ 4y – y ≤ y – y + 9

     ⇔ 3y ≤ 9

     ⇔ 1/3 x 3y ≤ 1/3 x 9

     ⇔ y ≤ 3

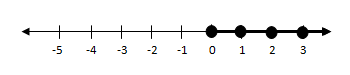
     Jadi himpunan penyelesaiannya adalah {0, 1, 2, 3)

     Dan penyelesaian dalam bentuk grafiknya adalah sebagai berikut:

6) Penerapan Persamaan dan Pertidaksamaan Linear Satu Variabel dalam kehupan sehari-hari

Untuk soal yang berbentuk cerita, maka langkah-langkah penyelesaiannya adalah sebagai berikut:

• Jika memerlukan diagram (sketsa), misalnya untuk soal yang berhubungan dengan geometri, buatlah (sketsa) dari kalimat terbuka.
• Membuat model matematika, artinya menerjemahkan kalimat cerita menjadi kalimat matematika dalam bentuk persamaan atau pertidaksamaan.
• Menyelesaikan persamaan atau pertidaksamaan.

Contoh:

Siswa kelas 7 SMPN 1 Parungpanjang akan mengadakan Study Tour Ke Borobudur. Dalam rombongan tersebut terdiri dari 7 bus dengan jumlah penumpang yang sama dengan 2 mobil yang berpenumpang 8 orang. Mereka membeli tiket masuk untuk seluruh peserta study tour sebanyak 366 tiket. Tentukan jumlah penumpang setiap bus!

Penyelesaian:

Jumlah Penumpang dalam mobil adalah 2 x 8 = 16 orang.

Jumlah penumpang setiap bus adalah p, maka kita memiliki persamaan:

7p + 16 = 366

⇔ 7p + 16 – 16 = 366 - 16

⇔ 7p = 350

⇔ 1/7 x 7p = 1/7 x 350

⇔ p = 50

Jadi banyaknya penumpang tiap bus adalah 50 orang.

Demikian pembahasan tentang Materi Pertidaksamaan Linear Satu Variabel (PtLSV). Silahkan Unduh materinya pada link di bawah. Selain itu anda bisa juga mengunduh materi sebelumnya yaitu pada link PLSV Part 1 dan PLSV Part 2, untuk melengkapi Materi Persamaan dan Pertidaksamaan Linear Satu Variabel.

Baca Juga : PLSV & PTLSV Part 1
Baca Juga : PLSV & PTLSV Part 2

Anda juga dapat mengunduh Rangkuman Materi tentang Pertidaksamaan Linear Satu Variabel pada link di bawah ini

Download Rangkuman Materi

Semoga bermanfaat dan dapat menambah sedikit ilmu serta kebaikan bagi kita.